Solving the "Miracle Sudoku" in Prolog

If you haven’t seen it already, you owe it to yourself to watch this video on “CrackingTheCryptic” of a competitive Sudoku solver working through the Miracle Sudoku puzzle:

Watching that video reminded me of a programming languages course I took, where we wrote a simple Sudoku solver in Prolog. Since Prolog is a declarative language, writing a Sudoku solver is remarkably concise. In essence, all the programmer needs to do is define the constraints of the game, and Prolog is smart enough to find solutions:

:- use_module(library(clpfd)).

sudoku(Rows) :-
    length(Rows, 9), maplist(same_length(Rows), Rows),
    append(Rows, Vs), Vs ins 1..9,
    maplist(all_different, Rows),
    transpose(Rows, Columns),
    maplist(all_different, Columns),
    Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
    blocks(As, Bs, Cs),
    blocks(Ds, Es, Fs),
    blocks(Gs, Hs, Is).

blocks([], [], []).
blocks([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
        all_different([N1,N2,N3,N4,N5,N6,N7,N8,N9]),
        blocks(Ns1, Ns2, Ns3).

The code above is from the SWI Prolog docs, which uses a Constraint Logic Programming extension. You can play around with it in the SWISH online Prolog environment.

The cool thing about this code is that it works both as a Sudoku solver and as a Sudoku generator. You can query it with a partially solved board, and it will find all valid solutions. This means that you can also give it an empty board, and Prolog will generate all possible Sudoku solutions (although, this will take some time as there are $6.7 \times 10^{21}$ valid boards¹).

As a disclaimer, I don’t know Prolog very well. I’ve only barely tinkered with it, so I’m sure that my usage of it is suboptimal. Despite this, I was able to write a working Miracle Sudoku solver. 😄

A Miracle Sudoku Solver

To write a solver for the Miracle Sudoku puzzle, we need to encode the following rules:

Normal Sudoku rules apply:
- All rows/columns must contain 1..9 exactly once.
- Each 3x3 block must contain 1..9 exactly once.
Any two cells separated by a knight’s move or king’s move cannot contain the same digit.
Any two orthogonally adjacent cells (i.e., cells sharing an edge) cannot contain consecutive digits.

The Orthogonal Adjacency constraint is the easiest to encode. For each 3x3 grid on the board, we need to make sure that the corners differ from their neighbors by at least one. (We use the corners instead of the middle to handle boundary cases at the edge of the grid.)

%- [[N1, N2, N3],
%-  [N4, N5, N6],
%-  [N7, N8, N9]]
ortho_adjacent([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
    abs(N1 - N2) #> 1, abs(N1 - N4) #> 1,
    abs(N3 - N2) #> 1, abs(N3 - N6) #> 1,
    abs(N7 - N4) #> 1, abs(N7 - N8) #> 1,
    abs(N9 - N8) #> 1, abs(N9 - N6) #> 1,
    append([N2, N3], Ns1, Z1),
    append([N5, N6], Ns2, Z2),
    append([N8, N9], Ns3, Z3),
    ortho_adjacent(Z1, Z2, Z3).
ortho_adjacent([_,_], [_,_], [_,_]). %- Base case

Next is the King’s Move constraint, which is just as simple. I decided to use the all_different function as a shortcut for inequality. We could have used the #\= operator on N5’s neighbors, but we also need to handle the edge cases of the grid, which is why we also need to constrain the corners – N1, N3, N7, and N9. Unfortunately, this creates some duplicate constraints.

%- [[N1, N2, N3],
%-  [N4, N5, N6],
%-  [N7, N8, N9]]
kings_move([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
        all_different([N1, N2, N4]), all_different([N4, N7, N8]),
        all_different([N2, N3, N6]), all_different([N8, N9, N6]),
        all_different([N5, N4, N2]), all_different([N2, N5, N6]),
        all_different([N5, N6, N7]), all_different([N4, N5, N8]),
        append([N2, N3], Ns1, Z1),
        append([N5, N6], Ns2, Z2),
        append([N8, N9], Ns3, Z3),
        kings_move(Z1, Z2, Z3).
kings_move([_,_], [_,_], [_,_]).

I initially thought the Knight’s Move constraint would be more difficult to write, but it turns out that it tiles just as well as the others: all of the “L” movements of a knight also fix within a 3x3 grid.

%- [[N1, N2, N3],
%-  [N4, N5, N6],
%-  [N7, N8, N9]]
knights_move([N1,N2,N3|Ns1], [N4,N5,N6|Ns2], [N7,N8,N9|Ns3]) :-
    N1 #\= N6, N1 #\= N8,
    N3 #\= N8, N3 #\= N4,
    N7 #\= N2, N7 #\= N6,
    N9 #\= N4, N9 #\= N2,
    append([N2, N3], Ns1, Z1),
    append([N5, N6], Ns2, Z2),
    append([N8, N9], Ns3, Z3),
    knights_move(Z1, Z2, Z3).
knights_move([_,_], [_,_], [_,_]).

Now that we’ve written relations for the Miracle Sudoku rules, we need to add them to the original sudoku function. Each function takes 3 rows at a time, and needs to operate over each window of three rows in the board. A verbose way to do this is as follows:

sudoku(Rows) :-
    ...
    Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
    ...
    ortho_adjacent(As, Bs, Cs),
    ortho_adjacent(Bs, Cs, Ds),
    ortho_adjacent(Cs, Ds, Es),
    ortho_adjacent(Ds, Es, Fs),
    ortho_adjacent(Es, Fs, Gs),
    ortho_adjacent(Fs, Gs, Hs),
    ortho_adjacent(Gs, Hs, Is),
    ...

We’re asserting the ortho_adjacent relation on rows (A, B, C), then on (B, C, D), and so on. We can use maplist to make this more compact:

sudoku(Rows) :-
    ...
    Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
    ...
    append(Chunk1,       [_, _], Rows),
    append([_|Chunk2],   [_],    Rows),
    append([_,_|Chunk3], [],     Rows),
    maplist(ortho_adjacent, Chunk1, Chunk2, Chunk3),
    maplist(knights_move,   Chunk1, Chunk2, Chunk3),
    maplist(kings_move,     Chunk1, Chunk2, Chunk3).

To explain: we use append to create 3 “chunks” of rows. Chunk1 is equivalent to [As,Bs,Cs,Ds,Es,Fs,Gs], Chunk2 is [Bs,Cs,Ds,Es,Fs,Gs, Hs], and Chunk3 is [Cs,Ds,Es,Fs,Gs,Hs,Is]. Then, we use maplist to apply these chunks to our relations. When you pass multiple lists to maplist, it calls the provided relation with the ith element of the jth list as an argument to the relation.

The notation from the maplist documentation explains its pattern of argument application:

maplist(P, [X11,...,X1n], ..., [Xm1,...,Xmn]) :-
    P(X11, ..., Xm1),
    ...
    P(X1n, ..., Xmn).

Now we have a concise way of describing the Miracle Sudoku problem in Prolog!

sudoku(Rows) :-
    length(Rows, 9), maplist(same_length(Rows), Rows),
    append(Rows, Vs), Vs ins 1..9,
    maplist(all_different, Rows),
    transpose(Rows, Columns),
    maplist(all_different, Columns),
    Rows = [As,Bs,Cs,Ds,Es,Fs,Gs,Hs,Is],
    blocks(As, Bs, Cs),
    blocks(Ds, Es, Fs),
    blocks(Gs, Hs, Is),
    append(Chunk1,       [_, _], Rows),
    append([_|Chunk2],   [_],    Rows),
    append([_,_|Chunk3], [],     Rows),
    maplist(ortho_adjacent, Chunk1, Chunk2, Chunk3),
    maplist(knights_move,   Chunk1, Chunk2, Chunk3),
    maplist(kings_move,     Chunk1, Chunk2, Chunk3).

Does it Work?

The original Miracle Sudoku from the video starts with this clue:

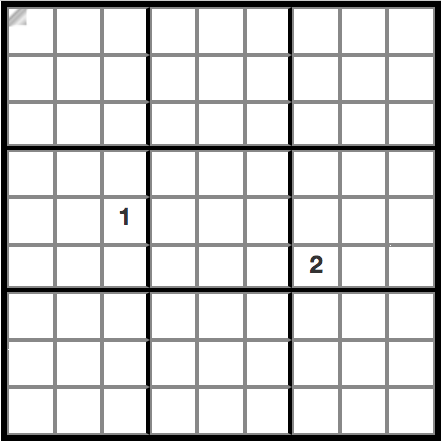
We can encode this problem in Prolog by creating a 9x9 board and populating it with the 2 digit hints. We leave the rest of the board as '_'s to let Prolog know that these are free variables. Our solver will keep the 1 and 2 in the positions that they’re set, but is free to choose any value for the rest of the '_'s, subject to the constraints of the puzzle.

problem(1, [[_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,1,_,_,_,_,_,_],
            [_,_,_,_,_,_,2,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_]]).

Now, we can query for solutions with our solver:

problem(1, Rows), sudoku(Rows), maplist(label, Rows), maplist(portray_clause, Rows).

Here’s what the query is doing:

problem(1, Rows) asserts that Rows must match the hint.
sudoku(Rows) asserts that the solution must match the Miracle Sudoku constraints.
maplist(label, Rows) tells Prolog to find concrete values for each of the free variables in Rows. (Otherwise, we just get a list of the constraints on each variable)
maplist(portray_clause, Rows) pretty prints the solution.

And the result?

?- problem(1, Rows), sudoku(Rows), maplist(labeling([ffc, enum]), Rows), maplist(portray_clause, Rows).

[4, 8, 3, 7, 2, 6, 1, 5, 9].
[7, 2, 6, 1, 5, 9, 4, 8, 3].
[1, 5, 9, 4, 8, 3, 7, 2, 6].
[8, 3, 7, 2, 6, 1, 5, 9, 4].
[2, 6, 1, 5, 9, 4, 8, 3, 7].
[5, 9, 4, 8, 3, 7, 2, 6, 1].
[3, 7, 2, 6, 1, 5, 9, 4, 8].
[6, 1, 5, 9, 4, 8, 3, 7, 2].
[9, 4, 8, 3, 7, 2, 6, 1, 5].

The solver works! To check that we didn’t just get lucky, it’d be nice to try this out against another instance of the puzzle. Fortunately, the CrackingTheCryptic channel later posted a follow-up video with a second puzzle:

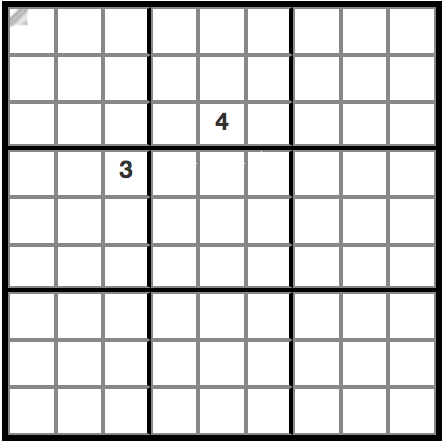
Plugging this into our solver, we’re able to find a solution quickly:

problem(2, [[_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,4,_,_,_,_],
            [_,_,3,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_]]).
problem(2, Rows), sudoku(Rows), maplist(label, Rows), maplist(portray_clause, Rows).

[9, 4, 8, 3, 7, 2, 6, 1, 5].
[3, 7, 2, 6, 1, 5, 9, 4, 8].
[6, 1, 5, 9, 4, 8, 3, 7, 2].
[4, 8, 3, 7, 2, 6, 1, 5, 9].
[7, 2, 6, 1, 5, 9, 4, 8, 3].
[1, 5, 9, 4, 8, 3, 7, 2, 6].
[8, 3, 7, 2, 6, 1, 5, 9, 4].
[2, 6, 1, 5, 9, 4, 8, 3, 7].
[5, 9, 4, 8, 3, 7, 2, 6, 1].

Correct again! One useful aspect of the Prolog solver is that it’s able to find all valid solutions for any given hint. In the Prolog REPL, once a solution has been found you can press ; to iterate to the next solution. In both of the above puzzles, the hint has exactly one valid solution. By definition, Sudoku puzzles should only have one solution, so these puzzles are in fact valid.

Generating Puzzles

Now that we have a solver for Miracle Sudoku problems, can we generate some of our own? To test this, I queried the solver with a completely blank board:

problem(3, [[_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_],
            [_,_,_,_,_,_,_,_,_]]).
problem(3, Rows), sudoku(Rows), maplist(label, Rows), maplist(portray_clause, Rows).

And the result? Well… nothing. Just the sound of my laptop’s fans spinning. I think that the way I’m instructing Prolog to search for solutions is too naive to generate boards without prompting. My bet is that maplist(label, Rows) is performing “guess and check” search of the entire space, which is much too slow to generate boards without the constraint of a hint.

It’s a bit disappointing not to be able to generate novel boards with this solver. Perhaps someone with more Prolog knowledge could implement a more efficient solution.

Digression: Picat

While writing this article, I stumbled upon Hakan Kjellerstrand’s Miracle Sudoku solver written in Picat, a logic-based programming language I’d never heard of before.

Hakan’s solver is much faster than mine – it’s so fast that it can generate all possible Miracle Sudoku boards in about the time it takes mine to solve a single puzzle instance. Surprisingly, there are only 72 solution boards that meet the Miracle Sudoku constraints². I know even less about Picat than I do about Prolog, so I’m not sure how Hakan’s solution is so much faster than mine.

I’d recommend reading through the Picat solver source code. Since Hakan’s solution is so fast, it’s able to discover a couple other interesting properties of the Miracle Sudoku puzzle:

The minimal number of hints necessary to uniquely define a solution board is 2.
Boards with just 1 placed hint have 8 solutions, always – no matter which digit the hint is or where it’s placed.
There are many, many valid 2-digit hints. For example, there are 2320 ways to place a 1 and a 2 on the board which lead to a unique solution. Since there are only 72 unique solution boards, you’d run out of interesting solutions before you ran out of hints.

Conclusion

I don’t have many uses for Prolog in my day-to-day work, but it’s fun to work in a (relatively) obscure language like this when it’s well suited for the task. I’ve made a mental note to check out Picat, too. Hakan’s site has a wealth of example problems with solutions.

I also had no idea that there were puzzle makers extending traditional Sudoku – there are over a dozen variants listed on its Wikipedia page. There’s ample fodder in the CrackingTheCryptic Youtube channel for puzzle variants to write solvers for.