You Need to be Wrong (Sometimes)

To be a well-calibrated predictor, you need to to be wrong (sometimes).

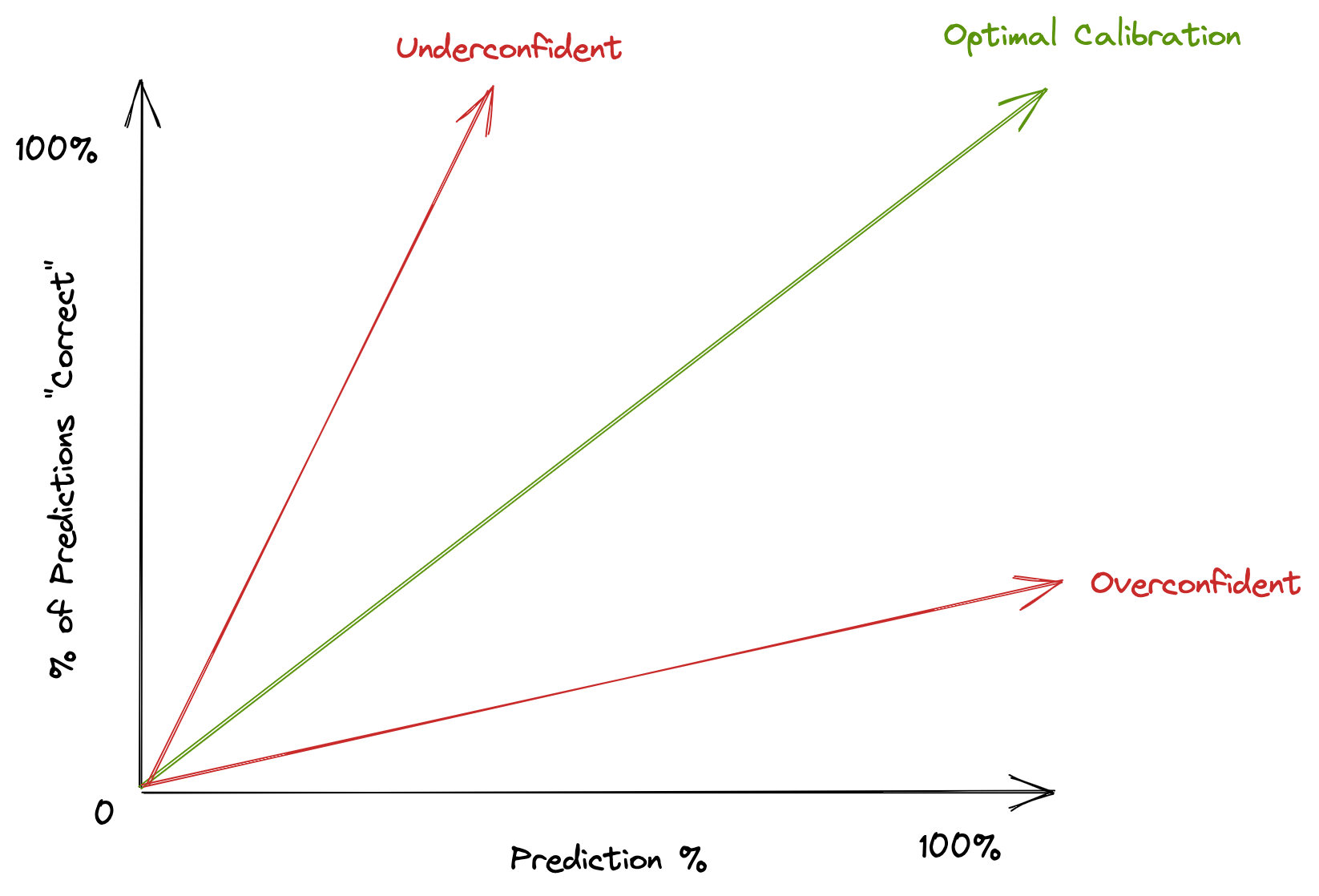
“Well-calibrated” means that if you predict something occurs with X% probability, then that event actually occurs X% of the time. Since predictions are often made on one-off events, another way of expressing calibration is that X% of predictions that you made with X% confidence should resolve in your favor. For example, if you make 100 predictions of 100 independent events, each with probability 75%, then you’d expect that (roughly) 75 of your predictions would be “correct”.

The corollary to this is that, in the same example, you’d expect that 25 of your predictions would be “wrong”. And this is a good thing. If you instead observed that only 5 of your predictions were “wrong”, then you would not be well-calibrated. Rather, you’d be significantly underconfident in your predictions.

I’ve been working for the past couple years to improve my prediction ability, and noticed that when I got a confident prediction wrong, I’d feel a sting of annoyance. For me, this threshold really sets in around 70%. If I’m >70% confident in my prediction, and it ends up being wrong, it feels bad.

The failure mode that I try to avoid is only making predictions that I’m actually very confident on, and then marking them down to, say, 70% confidence.¹ This may make you feel good – fewer “wrong” predictions! – but is the path towards an underconfident calibration curve.

To be well-calibrated, you need to be wrong – even of events that you assign a moderately high probability to.

Again, if you make 100 predictions, each with 70%, and you don’t get any of those wrong, then your 70% probability estimates were very likely incorrect². Being incorrect at the calibration level is worse than being wrong on any one event, because it indicates that your meta reasoning for assigning probabilities is inaccurate. Being “wrong” on any one event is itself not necessarily a problem. The world is stochastic. Even if your predictions are true representations of the probability of an outcome, this still means you’ll be wrong uncomfortably often.

Improving decision quality is about increasing our chances of good outcomes, not guaranteeing them.

– Thinking in Bets, by Annie Duke

Cover image: Discovery Park